The Role of the Data-Fidelity Term in Solving Linear Inverse Problems
The Data-Fidelity Term in Linear Inverse Problems
In some of our recent works, we investigate the role of the data-fidelity term in solving linear inverse problems. Most often in linear inverse problems, the $\ell_2$-norm is used to compute the error between the measurements and the measurement model. Consider the measurement model:
Here, $A$ is the forward operator (or sensing matrix) that describes the measurement process, and $w$ represents measurement noise. Since $A$ is often ill-conditioned or rectangular (with fewer measurements than signal dimensions), the problem is ill-posed and requires regularization to find a meaningful solution.
The standard approach is to solve an optimization problem with the $\ell_2$-norm as the data-fidelity metric:
Although this choice has statistical backing, i.e., the $\ell_2$-norm is a direct consequence of modelling additive noise as a Gaussian random variable in maximum a posteriori estimation, it is often not the best choice in practice
Introduction to Frames
In linear algebra, a basis for a vector space is a set of linearly independent vectors that span the space. This means any vector in the space can be written as a unique linear combination of the basis vectors. Frames are a generalization of bases that provide more flexibility. A frame is a set of vectors that also spans the space but is not required to be linearly independent. This redundancy can be highly beneficial for robustness to noise and errors.
Formally, a set of $N$ vectors $\lbrace v_i \in \mathbb{R}^n \rbrace_{i=1}^N$ is said to constitute a frame for $\mathbb{R}^n$ if there exist constants $0 < \alpha \le \beta < \infty$ such that for any vector $x \in \mathbb{R}^n$, the following condition holds:
The constants $\alpha$ and $\beta$ are called the frame bounds.
If the frame bounds are equal, $\alpha = \beta$, the frame is called a tight frame. If $\alpha = \beta = 1$, it is a Parseval tight frame. Tight frames share some of the desirable properties of orthonormal bases, making them particularly useful in areas like compressed sensing.
The Back-Projection Loss as a Distance Minimization
The back-projection loss is defined as the squared distance from a candidate solution $x$ to the solution space of the measurement model. Let’s define the solution space (in the noiseless case) as the affine subspace $C = \lbrace z \in \mathbb{R}^n : Az = y\rbrace$. This set contains all possible signals that are perfectly consistent with the measurements $y$.
The squared Euclidean distance from a point $x$ to this set is given by:
The point in $C$ closest to $x$ is the orthogonal projection of $x$ onto $C$, denoted as $\text{proj}_C(x)$. For a full row-rank matrix $A$, this projection is given by:
where $A^{\dagger} = A^T(AA^T)^{-1}$ is the Moore-Penrose pseudoinverse of $A$. Therefore, the squared distance is:
The back-projection loss is precisely this squared distance. The optimization problem then becomes:
This formulation seeks a solution that is not only regularized by $g(x)$ but is also minimally distant from the space of all signals that could have produced the measurements. Such a choice has been shown to provide superior reconstruction accuracy for inverse problems in imaging
Back-Projection and Tight Frames in Compressed Sensing
In compressed sensing (CS), the goal is to recover a sparse signal from a few measurements. The choice of the sensing matrix $A$ is critical. While random Gaussian matrices are easy to construct and satisfy theoretical guarantees like the Restricted Isometry Property (RIP), tight-frame matrices are known to yield the minimum mean-squared error. A matrix $V$ is a Parseval tight frame if $VV^\top = I$.
Minimum MSE Recovery with an Oracle
To understand why tight frames are optimal, consider an idealized scenario where an “oracle” tells us the exact locations (the support, denoted by $S$) of the non-zero entries in the sparse signal $x$. The recovery problem then simplifies to finding the values of these non-zero coefficients.
Let $x_S$ be the vector of non-zero values of $x$ and $A_S$ be the submatrix of $A$ containing only the columns indexed by the support $S$. The measurement model becomes:
This is a standard linear estimation problem. The best linear unbiased estimator for $x_S$ is the least-squares solution, which gives the recovered values $\hat{x}_S$:
The mean-squared error (MSE) of this estimate is directly related to the properties of the matrix $(A_S^T A_S)^{-1}$. The error is minimized when this matrix is well-conditioned. A tight-frame sensing matrix $A$ ensures that for any support $S$, the columns of $A_S$ are as close to orthogonal as possible, which makes $A_S^T A_S$ well-conditioned (close to the identity matrix). This minimizes the amplification of the noise $w$ during the recovery process, thus achieving the minimum possible MSE.
The Back-Projection Bridge
The back-projection loss provides a remarkable bridge between the convenience of random matrices and the optimality of tight frames. Consider the standard CS problem formulation with a non-tight sensing matrix $A$ (e.g., Gaussian) and the back-projection loss:
where $D$ is a sparsifying dictionary. This is equivalent to solving the problem with a modified data-fidelity term $\Vert B(Ax-y)\Vert^2_2$ where $B=(AA^T)^{-1/2}$.
This formulation is equivalent to solving the original problem with an effective sensing matrix $\tilde{A} = BA = (AA^T)^{-1/2}A$ and effective measurements $\tilde{y} = By$. The key insight is that this new sensing matrix $\tilde{A}$ is a Parseval tight frame, because:
This means that by simply changing the data-fidelity loss to the back-projection loss, we can gain the performance benefits of a tight-frame sensing matrix without the difficulty of constructing one. This leads to improved recovery guarantees, especially when the number of measurements is low or the signal is less sparse.
A Wiener-Filter-like Update for Image Deconvolution
When the forward model $A$ represents a convolution, such as in image deblurring, the back-projection loss has another elegant interpretation. In iterative optimization algorithms like the proximal gradient method, the update step involves computing the gradient of the data-fidelity term.
For the standard least-squares loss, the gradient is $\nabla f_{LS}(x) = A^T(Ax-y)$. For the back-projection loss, the gradient is $\nabla f_{BP}(x) = A^T(AA^T)^{-1}(Ax-y)$.
In practice, the matrix $AA^T$ can be ill-conditioned, so a regularized inverse is used. For a convolutional operator $H$, the gradient update becomes:
This expression is precisely the form of a Wiener filter. In the Fourier domain, if $\mathcal{F}(\cdot)$ is the Fourier transform, the operator $H^T(HH^T + \epsilon I)^{-1}$ becomes a filter with the frequency response:
where $h$ is the blur kernel. This filter adaptively de-emphasizes frequencies that were attenuated by the blur, preventing noise amplification. Therefore, using the back-projection loss in a convolutional setting is akin to incorporating a Wiener-filter-like deconvolution step directly into the gradient update of the optimization, leading to more stable and accurate reconstructions.
Solving Inverse Problems with the Method of Alternating Proximations
This optimization problem can be solved efficiently using the proximal gradient method (PGM). PGM is an iterative algorithm designed for problems that are a sum of a smooth function and a (possibly non-smooth) function for which we can compute a proximal operator.
In our case, the objective function is $f(x) + h(x)$, where $f(x) = \frac{1}{2} \Vert A^{\dagger}(y - Ax)\Vert_2^2$ is the smooth data-fidelity term, and $h(x) = \lambda g(x)$ is the regularization term.
The gradient of the smooth part is:
The PGM update step is given by:
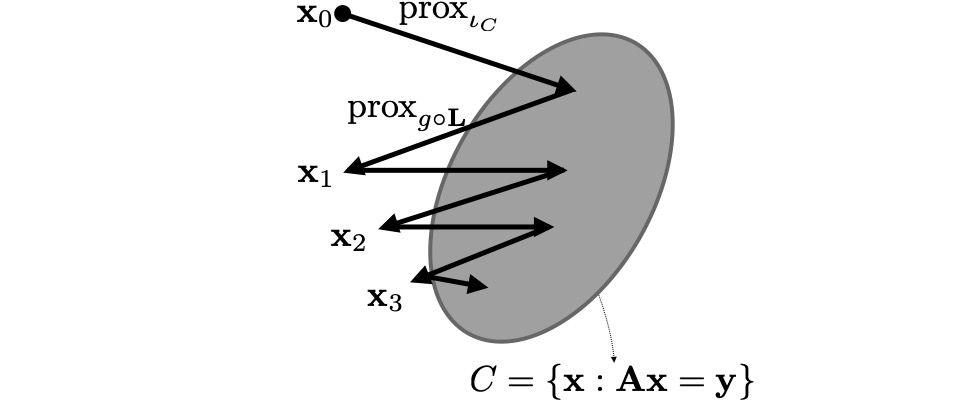
$x_{k+1} = \text{prox}_{\lambda g}(x_k - A^{\dagger}(Ax_k-y))$.
Notice that the term inside the proximal operator is exactly the projection of $x_k$ onto the solution space $C$:
This allows us to write the update in a very intuitive form:
The iterative scheme that follows the proximal gradient method can also be viewed from the perspective of alternating approximations
Empirically, it was observed that the method of alternating proximations provided faster and superior-quality reconstructions compared to the standard least-squares data-fidelity for compressive sensing